多变量线性回归(Linear Regression with Multiple Variables)
多维特征(Multiple Features)
定义:区别于单一特征向量,当存在多个特征向量去描述一个函数时,需要利用到多元特征向量去表示。多元特征向量的表示方法如下:
多元特征向量所表示的函数如下图所示:
上式中,可以假设存在一个X0=1来化简式子,得到下图。
多变量梯度下降(Gradient Descent for Mutiple Variables)
原理:构造出多特征线性规划后,我们可以通过梯度下降法对其进行求解,此时要选择代价函数J,使目标变量的真实值和预测值的距离最小,故选择最小二乘为代价函数。如下图
于是得到梯度下降的迭代公式:
运算,化简得到:
特征缩放(Feature Scaling)
特征缩放:为了使得梯度下降算法在使用的过程中更快收敛,我们在存在多个特征的机器学习的题目中,将各个特征的取值范围缩放到相近的范围,例如:[-1,1]。如图。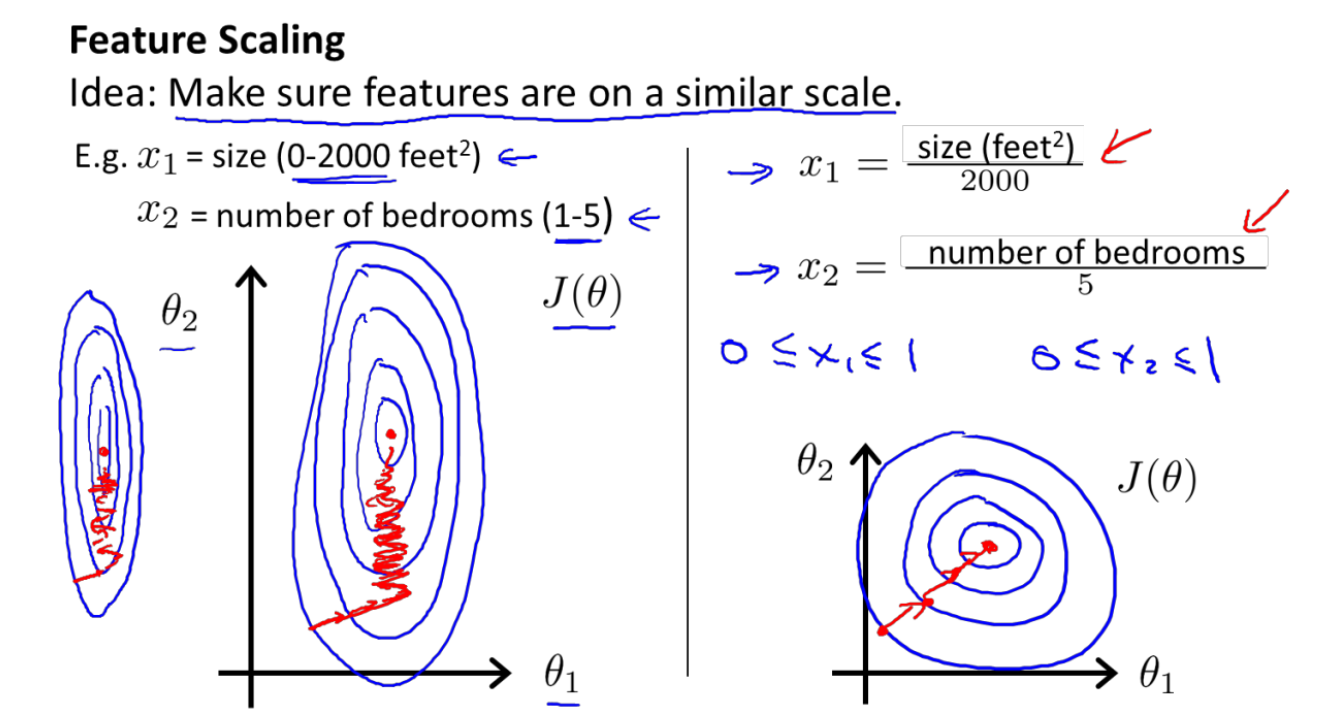
通常的,我们有Mean normalization:
$$x=\frac{x_i-\mu_i}{max-min}$$
通过特征缩放能使我们的梯度下降算法收敛得更快。
学习率(Learning Rate)
学习率a:我们可以通过对(代价函数最小值——梯度下降迭代次数)的函数图像进行分析,判断梯度下降算法的学习率a是否准确。如下图。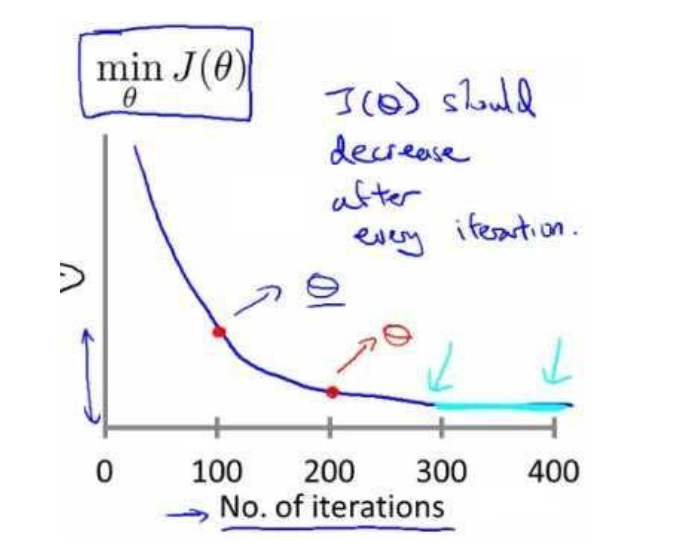
(1) 若是这个图像是递增的,说明这个学习率过大。
(2) 若是这个图像是递减且收敛缓慢,说明这个学习率过小。
(3) 若是这个图像是递减且很快收敛,说明这个学习率合适。
(P.S. 一般对学习率的选取可以选择3倍一取或10倍一取。)
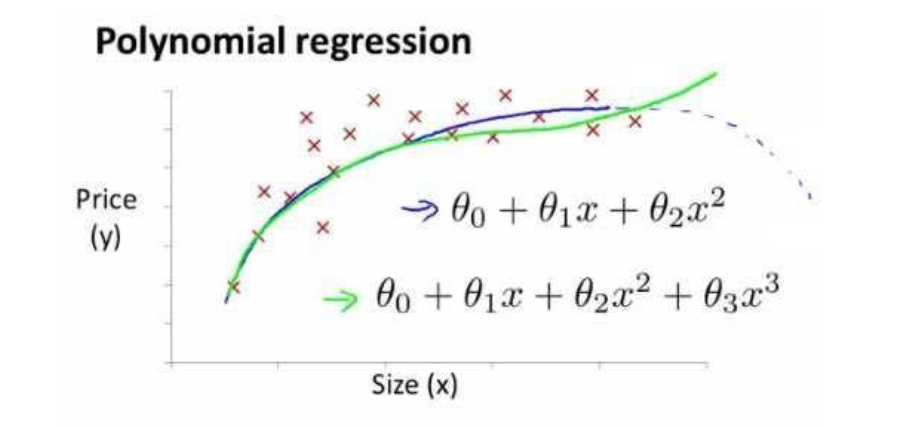
特征和多项式回归(Features and Polynomial Regression)
定义:在使用多元线性回归的时候,我们应该选取比较合适的模型对数据进行拟合,例如:一元二次函数或一元三次函数。如下图所示: