正规方程(Normal Equation)
正规方程:区别于梯度下降算法,是另一种解决线性回归问题的算法。是通过求解下面方程来找出使得代价函数最小的参数的:
$$\frac{\partial}{\partial\theta_j}J(\theta_j)$$
首先先介绍一些规范:
- 训练集特征矩阵为X(包含了$X_0=1$)。
- 训练集结果为向量y。
则正规方程求解后得到的向量为:
$$\theta = (X^TX)^{-1}X^Ty$$
举下列数据为例:
即
运用正规方程求解参数可得:
注意:对于不可逆的矩阵(通常是因为特征之间不独立,如同时包含英尺为单位的尺寸和米为单位的尺寸两个特征,也有可能是特征数量大于训练集的数量),正规方程方法是不能用的。
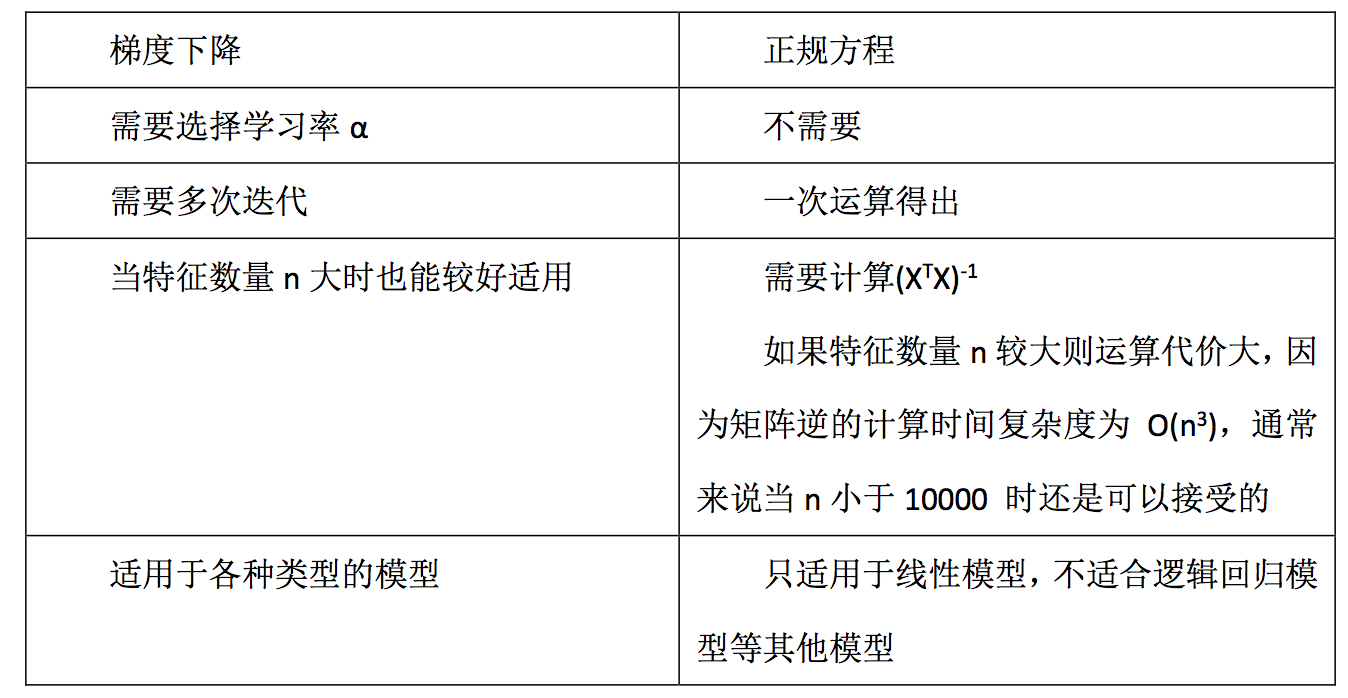
梯度下降和正规方程的对比: