单变量的线性回归(Linear Regression with One Variable)
其中,这里将讲解单变量的线性回归(Linear Regression with One Variable)。
首先,我们来看回之前总结过的预测房价的例子。见下图。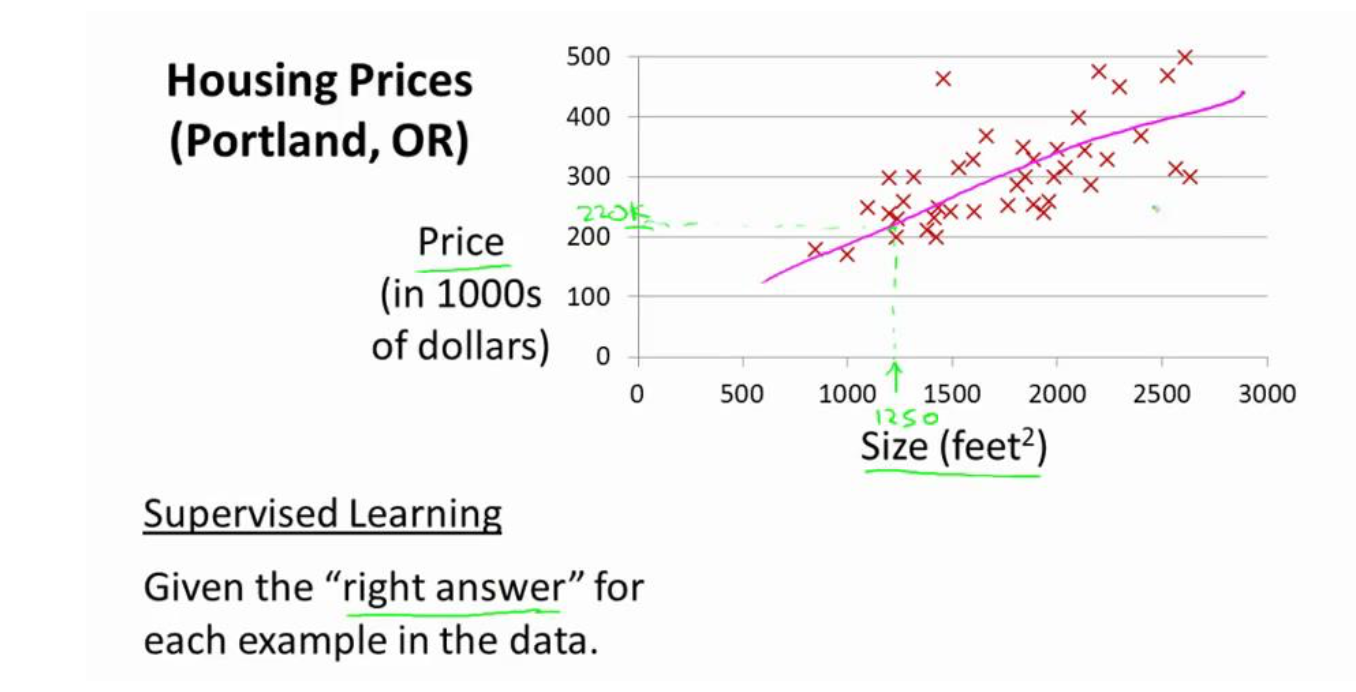
如图中所说,这里被归为监督学习的原因是,我们对每个数据都给出了“正确的答案”。而称为回归问题是因为我们能够根据之前的数据预测出一个准确的输出值,即房屋价格。
一般来说,在监督学习中,我们有一个数据集,这个数据集被称为训练集。以预测房价为例,见下图。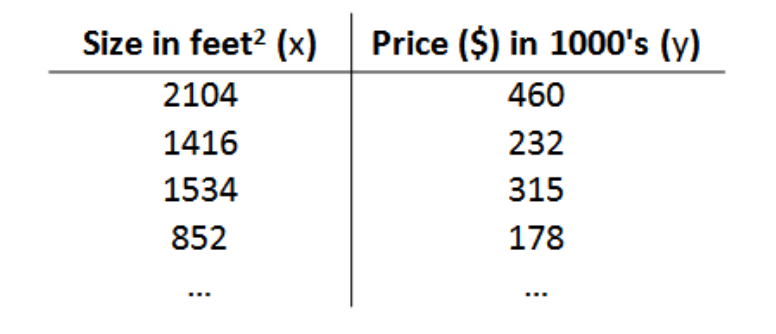
在回归问题中,我们对一些描述的标记如下所示:
m 代表训练集中实例的数量。
x 代表特征/输入变量
y 代表目标变量/输出变量
(x,y) 代表训练集中的实例
($x^{i}$,$y^{i}$) 代表第 i 个观察实例
h 代表学习算法的解决方案或函数也称为假设(hypothesis)
模型表示(Model Representation)
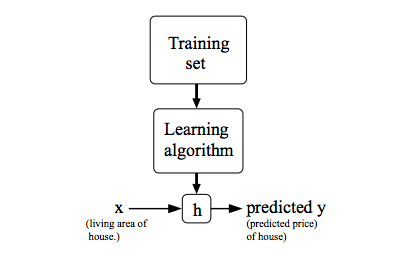
上图描述了一个监督学习算法的工作方式。同样举房屋例子来说,我们通过将训练集(即房屋价格及它们所对应的特征数据)作为输入投入学习算法中,学习算法工作后,会输出一个函数,记作h(即上文代表的hypothesis)。得到h之后,我们可以通过输入房屋的特征数据(即x值),输出房屋的价格(即y值)。因此,我们可以看出h实则是一个从x到y的映射。
h的表示:
一般来说,在单变量线性回归问题当中,我们将h表示为:
$$h_{\theta}(x)=\theta_0+\theta_1x$$
代价函数(Cost Function)
上面提到了我们用来预测的函数是$h_{\theta}(x)=\theta_0+\theta_1x$的形式。其中$\theta_0$和$\theta_1$是这个模型的参数。在这里分别为直线的斜率和在y轴上的截距。我们需要做的便是要为这个模型选择合适的参数,把直线和数据尽可能地相拟合起来。如下图所示。
这时,我们需要引入一个评估指标来衡量我们得到的直线预测得到的值和我们的训练集数据真实值之间的差距:建模误差(modeling error)。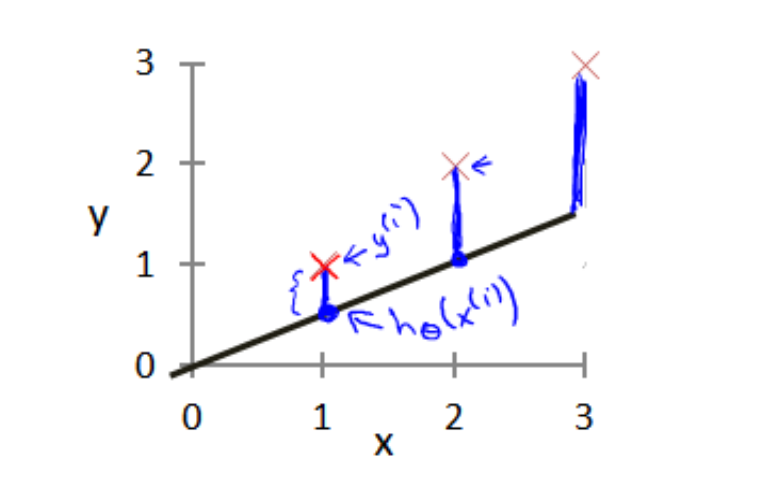
如上图所示,当我们通过将各个数据中的建模误差的平方求和之后,就能构建代价函数:
$$J(\theta_0, \theta_1)=\frac{1}{2m} \sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})^2$$
得到代价函数之后,我们的目标就转为了找到$\theta_0$和$\theta_1$的取值能够使得代价函数取到最小。如下图所示。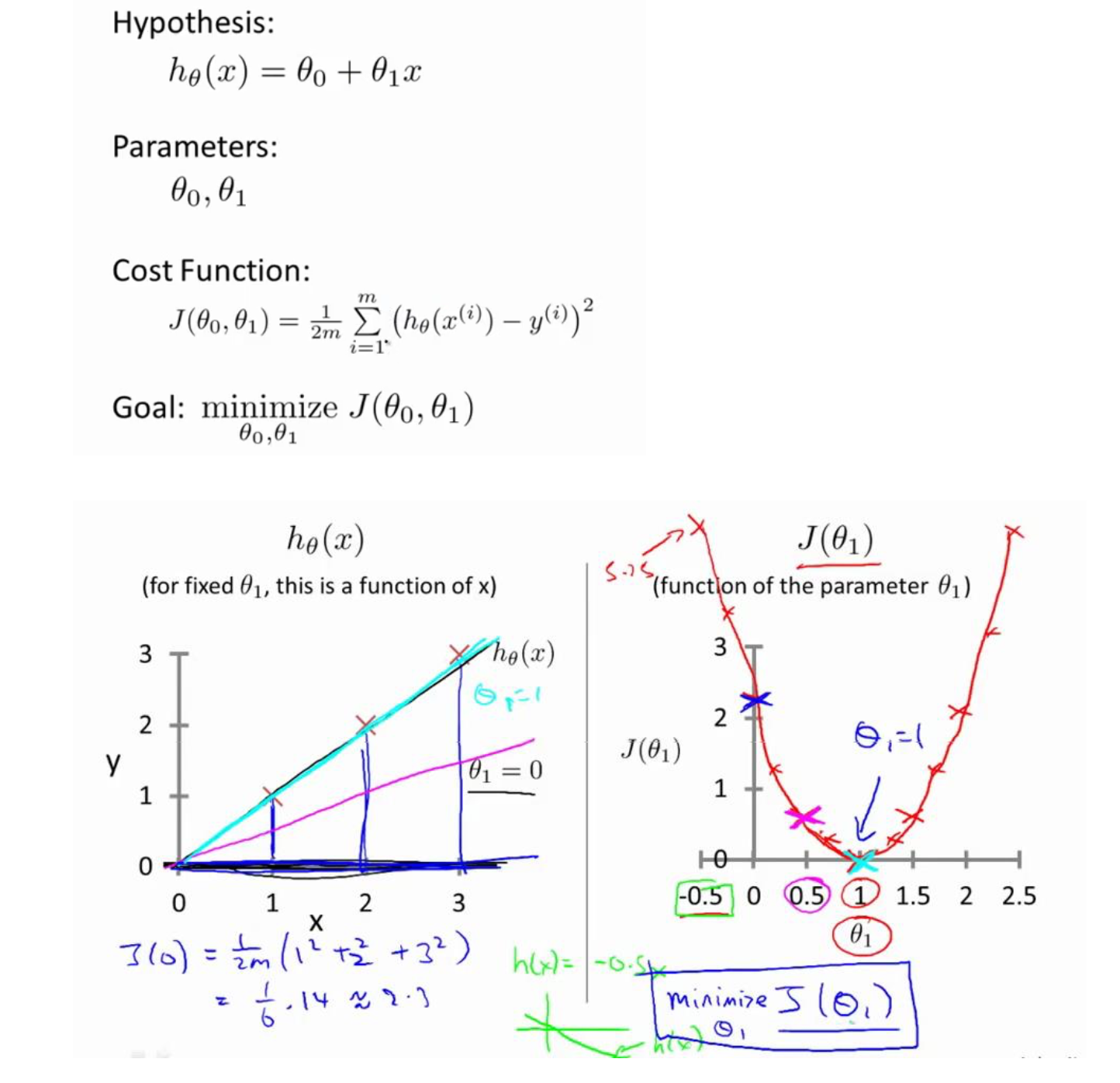
我们还可以通过等高线图来进行分析: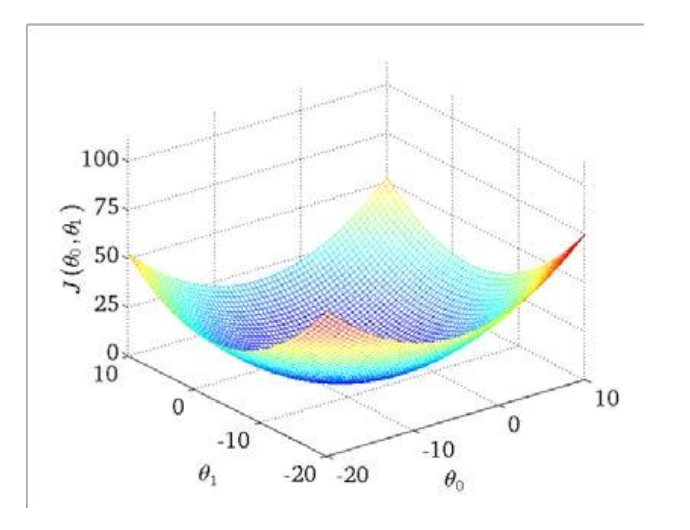
可以看出,在三维空间里,存在着使得$J(\theta_0,\theta_1)$最小的点。
一般来说,代价函数被称为平方误差函数。对于回归问题,是常用的合理的选择。
梯度下降(Gradient Descent)
梯度下降指的是一个用来求函数最小值的算法。我们可以使用它求出代价函数$J(\theta_0,\theta_1)$的最小值。
原理:通过一开始随机选择的参数组合($\theta_0,\theta_1,…,\theta_n$),计算代价函数,然后在这个过程中寻找下一个能让代价函数值下降最多的参数组合,直到找到一个局部最小值(local minimum)。当然,因为并没有将所有的参数组合全部尝试,所以我们不能确定的到的局部最小值就是全局最小值,而选择不同的初始参数组合,可能会找到不同的局部最小值。如下图所示。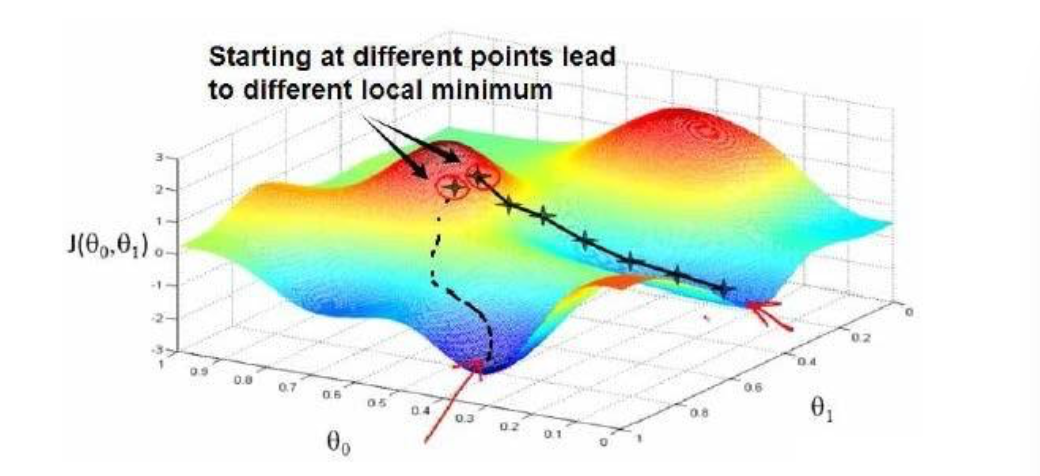
算法公式:
repeat until convergence {
$$\theta_j:=\theta_j - \alpha \frac{\partial}{\partial\theta_j}J(\theta)$$
}
其中,$\alpha$是学习率(learning rate),决定了沿着能让代价函数下降程度最大方向的每一个迭代的步伐有多大。
注意事项: 在梯度下降算法当中,我们需要更新参数值。而更新的过程必须要做到同时更新所有的参数项。例如,在单变量线性回归问题中我们需要同时更新$\theta_0$和$\theta_1$。如下图所示。
学习率(Learning Rate)
上面已经提及了学习率的基本概念,下面对学习率$\alpha$的相关知识进行解释。
首先$\alpha$的大小是可以调整的,通过调整$\alpha$的值,可以加快算法的运算,减少运算时间。但$\alpha$的值过大和过小会导致一些问题。
$\alpha$过大:会使得梯度下降的算法有可能一下子越过最低点,甚至可能导致无法收敛。
$\alpha$过小:会导致算法的运算时间过长,效率过低。
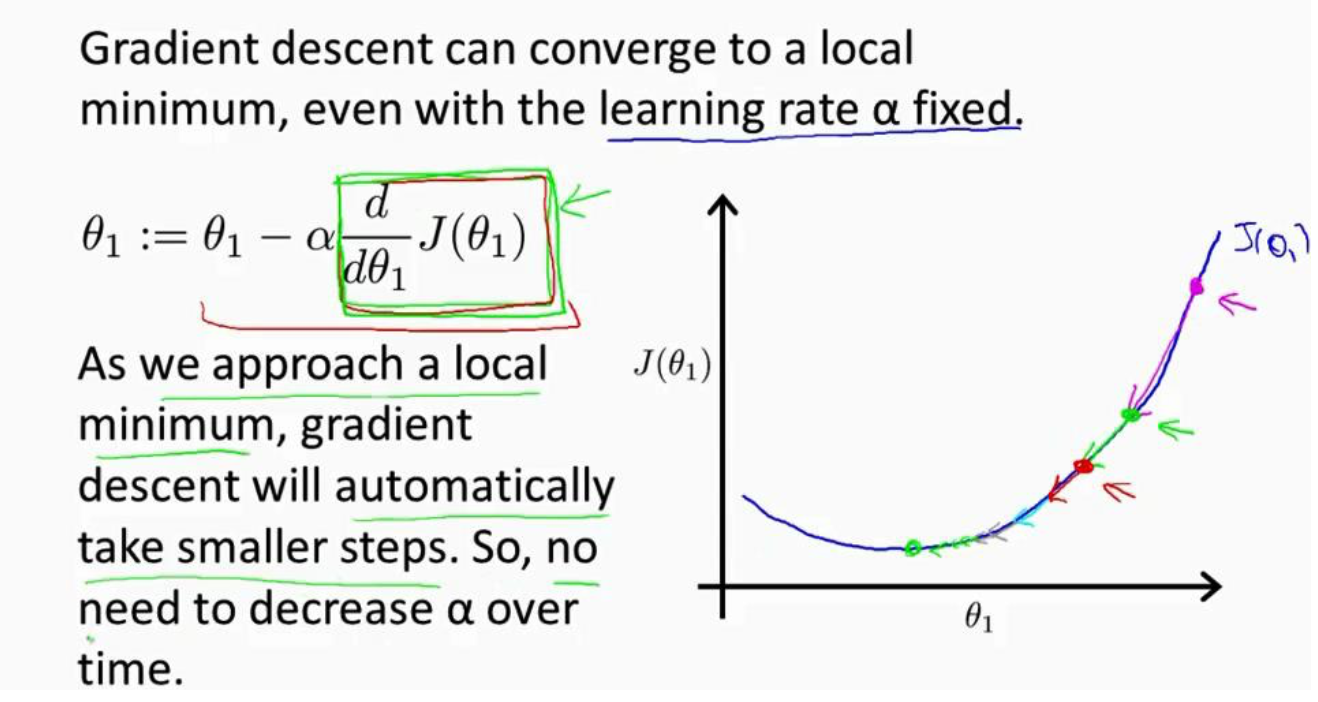
在梯度下降算法当中,$\alpha$的值没有必要减小,因为我们在每次迭代对梯度下降算法的参数$\theta$进行更新时,已经在原来的基础中将其更新幅度减小了,这样能够使得我们的算法收敛到我们想要的局部最小值。如下图。